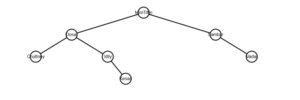
Python Trees
A tree is a hierarchical data structure consisting of nodes connected by edges.
Each node contains a value and references to its child nodes.
மரம் என்பது விளிம்புகளால் இணைக்கப்பட்ட முனைகளைக் கொண்ட ஒரு படிநிலைத் தரவுக் கட்டமைப்பாகும்.
ஒவ்வொரு முனையும் ஒரு மதிப்பையும், அதன் குழந்தை முனைகளுக்கான குறிப்புகளையும் கொண்டிருக்கும்.
Trees
The Tree data structure is similar to Linked Lists in that each node contains data and can be linked to other nodes.
Data structures like Arrays, Linked Lists, Stacks, and Queues. These are all linear structures, which means that each element follows directly after another in a sequence. Trees however, are different. In a Tree, a single element can have multiple ‘next’ elements, allowing the data structure to branch out in various directions.
The data structure is called a “tree” because it looks like a tree’s structure.
மரம் (Tree) தரவுக் கட்டமைப்பு, இணைக்கப்பட்ட பட்டியல்களைப் (Linked Lists) போன்றது. ஏனெனில், அதில் ஒவ்வொரு முனையும் தரவைக் கொண்டிருப்பதுடன், மற்ற முனைகளுடன் இணைக்கப்படவும் முடியும்.
அணிகள் (Arrays), இணைக்கப்பட்ட பட்டியல்கள், அடுக்குகள் (Stacks) மற்றும் வரிசைகள் (Queues) போன்ற தரவுக் கட்டமைப்புகள் அனைத்தும் நேரியல் கட்டமைப்புகள் ஆகும். அதாவது, ஒவ்வொரு உறுப்பும் ஒரு வரிசையில் மற்றொன்றைத் தொடர்ந்து நேரடியாக வருகிறது. இருப்பினும், மரங்கள் வேறுபட்டவை. ஒரு மரத்தில், ஒரு தனி உறுப்புக்கு பல ‘அடுத்த’ உறுப்புகள் இருக்க முடியும், இது தரவுக் கட்டமைப்பை பல்வேறு திசைகளில் கிளைத்துச் செல்ல அனுமதிக்கிறது.
இந்தத் தரவுக் கட்டமைப்பு ஒரு மரத்தின் அமைப்பைப் போலவே இருப்பதால், இது “மரம்” என்று அழைக்கப்படுகிறது.
Example / உதாரணம்
The Tree data structure can be useful in many cases:
Hierarchical Data: File systems, organizational models, etc.
Databases: Used for quick data retrieval.
Routing Tables: Used for routing data in network algorithms.
Sorting/Searching: Used for sorting data and searching for data.
Priority Queues: Priority queue data structures are commonly implemented using trees, such as binary heaps.
மரம் (Tree) தரவுக் கட்டமைப்பு பல சந்தர்ப்பங்களில் பயனுள்ளதாக இருக்கும்:
படிநிலைத் தரவு: கோப்பு அமைப்புகள், நிறுவன மாதிரிகள் போன்றவை.
தரவுத்தளங்கள்: தரவை விரைவாக மீட்டெடுக்கப் பயன்படுகிறது.
வழித்தட அட்டவணைகள்: நெட்வொர்க் வழிமுறைகளில் தரவை வழிநடத்தப் பயன்படுகிறது.
வரிசைப்படுத்துதல்/தேடுதல்: தரவை வரிசைப்படுத்தவும், தரவைத் தேடவும் பயன்படுகிறது.
முன்னுரிமை வரிசைகள்: பைனரி ஹீப்ஸ் போன்ற மரங்களைப் பயன்படுத்தி முன்னுரிமை வரிசை தரவுக் கட்டமைப்புகள் பொதுவாகச் செயல்படுத்தப்படுகின்றன.
Types of Trees
Trees are a fundamental data structure in computer science, used to represent hierarchical relationships. This tutorial covers several key types of trees.
Binary Trees: Each node has up to two children, the left child node and the right child node. This structure is the foundation for more complex tree types like Binay Search Trees and AVL Trees.
Binary Search Trees (BSTs): A type of Binary Tree where for each node, the left child node has a lower value, and the right child node has a higher value.
AVL Trees: A type of Binary Search Tree that self-balances so that for every node, the difference in height between the left and right subtrees is at most one. This balance is maintained through rotations when nodes are inserted or deleted.
மரங்களின் வகைகள்
மரங்கள் என்பவை கணினி அறிவியலில் படிநிலைத் தொடர்புகளைக் குறிக்கப் பயன்படும் ஒரு அடிப்படைத் தரவுக் கட்டமைப்பாகும். இந்த வழிகாட்டிப் பாடம் பல முக்கிய மர வகைகளைப் பற்றி விளக்குகிறது.
இருநிலை மரங்கள்: ஒவ்வொரு முனையத்திற்கும் இடது குழந்தை முனை மற்றும் வலது குழந்தை முனை என அதிகபட்சம் இரண்டு குழந்தைகள் இருக்கும். இந்த அமைப்பு, இருநிலை தேடல் மரங்கள் மற்றும் AVL மரங்கள் போன்ற மிகவும் சிக்கலான மர வகைகளுக்கு அடிப்படையாக அமைகிறது.
இருநிலை தேடல் மரங்கள் (BSTகள்): இது ஒரு வகை இருநிலை மரம் ஆகும். இதில் ஒவ்வொரு முனைக்கும், இடது குழந்தை முனையானது குறைந்த மதிப்பையும், வலது குழந்தை முனையானது அதிக மதிப்பையும் கொண்டிருக்கும்.
AVL மரங்கள்: இது ஒரு வகை இருநிலை தேடல் மரம் ஆகும். இது தானாகவே சமநிலைப்படுத்திக் கொள்ளும். இதனால் ஒவ்வொரு முனைக்கும், இடது மற்றும் வலது துணை மரங்களுக்கு இடையிலான உயர வேறுபாடு அதிகபட்சம் ஒன்றாக இருக்கும். முனைகள் சேர்க்கப்படும்போதோ அல்லது நீக்கப்படும்போதோ, சுழற்சிகள் மூலம் இந்தச் சமநிலை பராமரிக்கப்படுகிறது.
Trees vs Arrays and Linked Lists
Benefits of Trees over Arrays and Linked Lists:
- Arrays are fast when you want to access an element directly, like element number 700 in an array of 1000 elements for example. But inserting and deleting elements require other elements to shift in memory to make place for the new element, or to take the deleted elements place, and that is time consuming.
- Linked Lists are fast when inserting or deleting nodes, no memory shifting needed, but to access an element inside the list, the list must be traversed, and that takes time.
- Trees, such as Binary Trees, Binary Search Trees and AVL Trees, are great compared to Arrays and Linked Lists because they are BOTH fast at accessing a node, AND fast when it comes to deleting or inserting a node, with no shifts in memory needed.
மரங்கள் மற்றும் அணிவரிசைகள், இணைக்கப்பட்ட பட்டியல்களுக்கு இடையேயான ஒப்பீடு
அணிவரிசைகள் மற்றும் இணைக்கப்பட்ட பட்டியல்களை விட மரங்களின் நன்மைகள்:
- ஒரு அணிவரிசையில் உள்ள 1000 உறுப்புகளில் 700வது உறுப்பு போன்ற ஒரு உறுப்பை நேரடியாக அணுக விரும்பும்போது, அணிவரிசைகள் வேகமானவை. ஆனால், உறுப்புகளைச் செருகுவதற்கும் நீக்குவதற்கும், புதிய உறுப்பிற்கு இடம் கொடுக்க அல்லது நீக்கப்பட்ட உறுப்பின் இடத்தை நிரப்ப, மற்ற உறுப்புகள் நினைவகத்தில் இடம் மாற வேண்டியுள்ளது, இது அதிக நேரம் எடுக்கும்.
- இணைக்கப்பட்ட பட்டியல்களில் முனைகளைச் செருகும்போது அல்லது நீக்கும்போது வேகம் அதிகமாக இருக்கும், நினைவகத்தில் இடம் மாற்ற வேண்டியதில்லை. ஆனால், பட்டியலில் உள்ள ஒரு உறுப்பை அணுக, பட்டியல் முழுவதையும் கடந்து செல்ல வேண்டும், இதற்கு நேரம் எடுக்கும்.
- பைனரி மரங்கள், பைனரி தேடல் மரங்கள் மற்றும் AVL மரங்கள் போன்ற மரங்கள், அணிவரிசைகள் மற்றும் இணைக்கப்பட்ட பட்டியல்களுடன் ஒப்பிடும்போது சிறந்தவை. ஏனெனில் அவை ஒரு முனையை அணுகுவதிலும் வேகமானவை, மேலும் ஒரு முனையை நீக்குவதிலும் அல்லது செருகுவதிலும் வேகமானவை, இதற்கு நினைவகத்தில் எந்த இட மாற்றமும் தேவையில்லை.