Python Binary Trees

A tree is a hierarchical data structure consisting of nodes connected by edges.

Each node contains a value and references to its child nodes.

மரம் என்பது விளிம்புகளால் இணைக்கப்பட்ட முனைகளைக் கொண்ட ஒரு படிநிலைத் தரவுக் கட்டமைப்பாகும்.

ஒவ்வொரு முனையும் ஒரு மதிப்பையும், அதன் குழந்தை முனைகளுக்கான குறிப்புகளையும் கொண்டிருக்கும்.

 

Binary Trees

A Binary Tree is a type of tree data structure where each node can have a maximum of two child nodes, a left child node and a right child node.

 

This restriction, that a node can have a maximum of two child nodes, gives us many benefits:

• Algorithms like traversing, searching, insertion and deletion become easier to understand, to implement, and run faster.
• Keeping data sorted in a Binary Search Tree (BST) makes searching very efficient.
• Balancing trees is easier to do with a limited number of child nodes, using an AVL Binary Tree for example.
• Binary Trees can be represented as arrays, making the tree more memory efficient.

இருநிலை மரங்கள்

ஒரு இருநிலை மரம் என்பது ஒரு வகை மரத் தரவுக் கட்டமைப்பாகும், இதில் ஒவ்வொரு முனையத்திற்கும் அதிகபட்சமாக இரண்டு துணை முனைகள் இருக்கலாம், அவை இடது துணை முனை மற்றும் வலது துணை முனை ஆகும்.

 

ஒரு முனையத்திற்கு அதிகபட்சமாக இரண்டு துணை முனைகள் மட்டுமே இருக்க முடியும் என்ற இந்த வரம்பு, நமக்கு பல நன்மைகளைத் தருகிறது:

 

• மரம் வழிசெல்லல், தேடல், செருகல் மற்றும் நீக்குதல் போன்ற நெறிமுறைகள் புரிந்துகொள்ளவும், செயல்படுத்தவும் எளிதாகின்றன, மேலும் வேகமாக இயங்குகின்றன.
• ஒரு இருநிலைத் தேடல் மரத்தில் (BST) தரவுகளை வரிசைப்படுத்தி வைப்பது, தேடலை மிகவும் திறமையானதாக ஆக்குகிறது.
• குறைந்த எண்ணிக்கையிலான துணை முனைகளைக் கொண்டு மரங்களைச் சமநிலைப்படுத்துவது எளிது; உதாரணமாக, ஒரு AVL இருநிலை மரத்தைப் பயன்படுத்தலாம்.
• இருநிலை மரங்களை அணிவரிசைகளாகக் குறிப்பிட முடியும், இது மரத்தை நினைவகத் திறனுள்ளதாக்குகிறது.

 

 

 

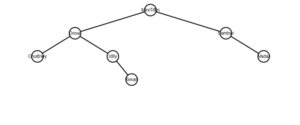
The Binary Tree above can be implemented much like a Linked List, except that instead of linking each node to one next node, we create a structure where each node can be linked to both its left and right child nodes.

மேலே உள்ள பைனரி மரத்தை ஒரு இணைக்கப்பட்ட பட்டியலைப் போலவே செயல்படுத்தலாம். ஆனால், ஒவ்வொரு முனையையும் அடுத்த ஒரு முனையுடன் இணைப்பதற்குப் பதிலாக, ஒவ்வொரு முனையும் அதன் இடது மற்றும் வலது குழந்தை முனைகள் இரண்டையுமே இணைக்கக்கூடிய ஒரு கட்டமைப்பை நாம் உருவாக்குகிறோம்.

 

Example:

class TreeNode:

def init(self, data):

self.data = data

self.left = None

self.right = None

 

root = TreeNode(‘MiniTiffin’)

nodeA = TreeNode(‘Dosai’)

nodeB = TreeNode(‘Sambar’)

nodeC = TreeNode(‘Chuttney’)

nodeD = TreeNode(‘Idlly’)

nodeE = TreeNode(‘Kesari’)

nodeF = TreeNode(‘Vadai’)

 

 

root.left = nodeA

root.right = nodeB

 

nodeA.left = nodeC

nodeA.right = nodeD

 

nodeD.right = nodeE

nodeB.right = nodeF

 

 

 

Test

print(“root.right.left.data:”, root.right.right.data)

Output:

root.right.right.data: Vadai

Types of Binary Trees

There are different variants, or types, of Binary Trees worth discussing to get a better understanding of how Binary Trees can be structured.

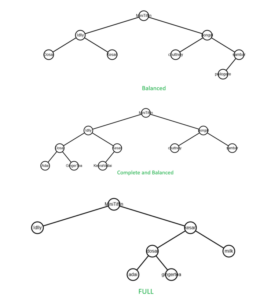
A balanced Binary Tree has at most 1 in difference between its left and right subtree heights, for each node in the tree.

A complete Binary Tree has all levels full of nodes, except the last level, which is can also be full, or filled from left to right. The properties of a complete Binary Tree means it is also balanced.

A full Binary Tree is a kind of tree where each node has either 0 or 2 child nodes.

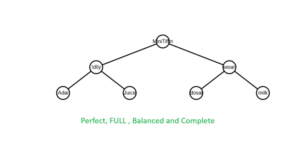
A perfect Binary Tree has all leaf nodes on the same level, which means that all levels are full of nodes, and all internal nodes have two child nodes.The properties of a perfect Binary Tree means it is also full, balanced, and complete.

இருநிலை மரங்களின் வகைகள்

இருநிலை மரங்கள் எவ்வாறு கட்டமைக்கப்படலாம் என்பதைப் பற்றி நன்கு புரிந்துகொள்ள, விவாதிக்கத் தகுந்த இருநிலை மரங்களின் பல்வேறு வகைகள் உள்ளன.

 

ஒரு சமச்சீர் இருநிலை மரத்தில், மரத்தில் உள்ள ஒவ்வொரு முனையத்திற்கும், அதன் இடது மற்றும் வலது துணை மரங்களின் உயரங்களுக்கு இடையே அதிகபட்சமாக 1 மட்டுமே வேறுபாடு இருக்கும்.

 

ஒரு முழுமையான இருநிலை மரத்தில், கடைசி நிலை தவிர மற்ற எல்லா நிலைகளிலும் முனைகள் முழுமையாக நிரம்பியிருக்கும். கடைசி நிலையும் முழுமையாக நிரம்பியிருக்கலாம் அல்லது இடமிருந்து வலமாக நிரப்பப்பட்டிருக்கலாம். ஒரு முழுமையான இருநிலை மரத்தின் பண்புகள், அது சமச்சீரானதாகவும் இருப்பதைக் குறிக்கிறது.

 

ஒரு முழு இருநிலை மரம் என்பது, ஒவ்வொரு முனையும் 0 அல்லது 2 குழந்தை முனைகளைக் கொண்ட ஒரு வகை மரமாகும்.

 

ஒரு பரிபூரண இருநிலை மரத்தில், அனைத்து இலை முனைகளும் ஒரே மட்டத்தில் இருக்கும். இதன் பொருள், அனைத்து நிலைகளும் முனைகளால் முழுமையாக நிரம்பியிருக்கும், மேலும் அனைத்து உள் முனைகளுக்கும் இரண்டு குழந்தை முனைகள் இருக்கும். ஒரு பரிபூரண இருநிலை மரத்தின் பண்புகள், அது முழுமையானது, சமச்சீரானது மற்றும் முழுமையான இருநிலை மரம் என்பதையும் குறிக்கிறது.

 

Binary trees that satisfies the following properties for every node:

 

• The left subtree of the node contains only nodes with keys lesser than the node’s key
• The right subtree of the node contains only nodes with keys greater than the node’s key
• The left and right subtree each must also be a binary search tree.

ஒவ்வொரு முனையத்திற்கும் பின்வரும் பண்புகளைப் பூர்த்தி செய்யும் இருமத் தேடல் மரங்கள்:

 

• அந்த முனையின் இடது துணைமரம், அந்த முனையின் திறவுகோலை விடச் சிறிய திறவுகோல்களைக் கொண்ட முனைகளை மட்டுமே கொண்டிருக்கும்.
• அந்த முனையின் வலது துணைமரம், அந்த முனையின் திறவுகோலை விடப் பெரிய திறவுகோல்களைக் கொண்ட முனைகளை மட்டுமே கொண்டிருக்கும்.
• இடது மற்றும் வலது துணைமரங்கள் ஒவ்வொன்றும் ஒரு இருமத் தேடல் மரமாகவும் இருக்க வேண்டும்.

 

 

In this  article, we focus more on the case where the keys of the nodes are represented by strings and not numbers. In this case, we should first define the ordering of the strings.

 

Lexicographic ordering is defined as the order that each string that appears in a dictionary. To determine which string is lexicographically larger we compare the corresponding characters of the two strings from left to right. The first character where the two strings differ determines which string comes first. Characters are compared using the Unicode character set and all uppercase letters come before lowercase letters.

 

இந்தக் கட்டுரையில், நோடுகளின் சாவிகள் எண்களால் அல்லாமல் சரங்களால் குறிப்பிடப்படும் நேர்வில் நாங்கள் அதிக கவனம் செலுத்துகிறோம். இந்த நேர்வில், நாம் முதலில் சரங்களின் வரிசையை வரையறுக்க வேண்டும்.

 

அகராதியில் ஒவ்வொரு சரமும் தோன்றும் வரிசையே அகரவரிசைப்படி வரிசைப்படுத்துதல் என வரையறுக்கப்படுகிறது. எந்தச் சரம் அகரவரிசைப்படி பெரியது என்பதைக் கண்டறிய, நாம் இரண்டு சரங்களின் தொடர்புடைய எழுத்துக்களை இடமிருந்து வலமாக ஒப்பிடுகிறோம். இரண்டு சரங்களும் வேறுபடும் முதல் எழுத்து, எந்தச் சரம் முதலில் வரும் என்பதைத் தீர்மானிக்கிறது. எழுத்துக்கள் யூனிகோடு எழுத்துத் தொகுப்பைப் பயன்படுத்தி ஒப்பிடப்படுகின்றன, மேலும் அனைத்து பெரிய எழுத்துக்களும் சிறிய எழுத்துக்களுக்கு முன்பாக வருகின்றன.

Binary Tree Traversal

Since Arrays and Linked Lists are linear data structures, there is only one obvious way to traverse these: start at the first element, or node, and continue to visit the next until you have visited them all.

But since a Tree can branch out in different directions (non-linear), there are different ways of traversing Trees.

இருநிலை மரத்தை கடந்து செல்லும் முறைகள்

அரேக்கள் மற்றும் இணைக்கப்பட்ட பட்டியல்கள் நேரியல் தரவு அமைப்புகள் என்பதால், அவற்றை கடந்து செல்ல ஒரே ஒரு தெளிவான வழி மட்டுமே உள்ளது: முதல் உறுப்பு அல்லது முனையத்திலிருந்து தொடங்கி, அனைத்து உறுப்புகளையும் பார்வையிடும் வரை அடுத்தடுத்தவற்றைத் தொடர்ந்து பார்வையிடுவது.

 

ஆனால் ஒரு மரம் வெவ்வேறு திசைகளில் கிளைக்கக்கூடும் என்பதால் (நேரியல் அல்லாதது), மரங்களைக் கடந்து செல்ல வெவ்வேறு வழிகள் உள்ளன.