முக்கோணவியல் – வெக்டார் கணிதம்

பொதுவாக எண்களை மட்டும் கையாள முக்கோணவியல் தேவையில்லை. ‘இரண்டும் மூன்றும் சமமா?’ என்று கேட்டால் இல்லை எனக் கூறி விடுவோம். ஆனால் (1,2) என்பதும் (2,3) என்பதும் சமமா எனக் கேட்டால் அப்போதுதான் முக்கோணவியல் நோக்கிச் செல்வோம். உடனே ஒரு graph போட்டு (1,2) க்கு ஒரு புள்ளியும் (2,3) ஒரு புள்ளியும் வைத்து நமது கணக்கீடுகளைத் துவங்குவோம். அங்குதான் முக்கோணவியல் அறிமுகம் ஆகிறது. இதுபோன்ற set of எண்களுக்கு வெக்டர் என்று பெயர். இதில் உள்ள ஒவ்வொரு எண்ணும் ஒவ்வொரு டைமென்ஷனில் உள்ள மதிப்பை குறிக்கிறது. எஜமான் படத்தில் ஹீரோவும் வில்லனும் தன்னை அறிமுகம் செய்து கொள்ளும் காட்சியில் “நான் பாசமானவன் நல்லவன்! நான் மோசமானவன் கெட்டவன்!” என்று இரண்டிரண்டு பண்புகளாக வைத்து தங்களை அறிமுகம் செய்து கொள்வார்களே! அதைப்போல! இரண்டிரண்டு எலிமெண்ட்ஸ் கொண்டது 2D வெக்டர். அதைக் குறிக்க X-அச்சு, Y-அச்சு போதும்! மூன்று எலிமெண்ட்ஸ் கொண்டது 3D வெக்டர். அதற்கு Z-அச்சும் சேர்ந்து கொள்கிறது. ஆனால் அதற்கும் மேல் எலிமெண்ட்ஸ் கொண்டவற்றை வரைபடம் வரைந்து குறிப்பது நடைமுறையில் இல்லை. நம்முடைய embedding மூலம் உருவாக்கப்படும் வெக்டரோ 100 எலிமெண்ட்ஸ் கொண்டவை. ஆகவே A, B, C என Z வரை அச்சுகள் சென்றாலும் நமக்குப் பத்தாது. இதுபோன்ற ஹையர் டைமென்ஷன் கொண்ட வெக்டர்களுக்கென்றே உருவாக்கப்பட்ட கணிதம் தான் வெக்டார் கணிதம். இதை முக்கோணவியல் அடிப்படைகளின் ஹையர் டைமென்ஷன் எனலாம். இரு வார்த்தைகளுக்கிடையேயான தொடர்பைக் கண்டுபிடிக்க, வெக்டார் கணிதத்தில் பயன்படும் வாய்ப்பாடு, முக்கோணவியல் அடிப்படைகளின் நீட்சியாகவே உள்ளது.

ஆகவே முதலில் 2D டைமென்ஷன் கொண்ட சிறிய அளவு வெக்டர்களை எடுத்துக்கொண்டு, முக்கோணவியலில் உள்ள தத்துவங்களை பற்றிப் புரிந்து கொள்வோம். பின்னர் இதே விஷயம் தான் 100D கொண்ட வெக்டருக்கு வெக்டார் கணிதத்தில் நிகழ்கிறது என்பதை சுலபமாகப் புரிந்து கொள்ளலாம்.

பொதுவாக ஒரு வெக்டர் என்பதற்கு எண் மதிப்பும் திசையும் இருக்கும். எல்லாவற்றையும் வெறும் எண்களால் குறிக்க முடியாதல்லவா! உதாரணத்துக்கு, “செங்கல்பட்டு to காஞ்சிபுரம் எப்படிச் செல்ல வேண்டும்?” எனக் கேட்டால் “40 கிலோமீட்டர் செல்லுங்கள்” என்று மொட்டையாக கூற முடியாது. நேராகச் சொல்ல வேண்டுமா? திரும்பிச் செல்ல வேண்டுமா? அல்லது எந்தத் திசையில் செல்ல வேண்டும்? என்று கூறினால்தான், அந்த விவரம் முழுமையடையும். அதுபோன்ற ஒரு சில இடங்களில், இந்த வெக்டர் அலகு முறை பயன்படுகிறது. இங்கும் வெக்டர்களாக மாற்றப்பட்ட வார்த்தைகள் சமமானவையா? எதிரானவையா? என்பதைக் கண்டுபிடிப்பதில் நமது வெக்டர்களின் திசை பெரும்பங்கு வகிக்கிறது.

உதாரணத்துக்கு இரு 2D வெக்டர்களை எடுத்துக்கொள்வோம். (1,2) என்பதும் (2,3) என்பதும் சமமா எனக் கேட்டால்,

• (1,2) -க்கு ஒரு புள்ளி வைத்து (0,0) -விலிருந்து ஒரு கோடு வரைவோமே, அதுதான் அதற்கான வெக்டர்.
• (2,3) -க்கு ஒரு புள்ளி வைத்து (0,0) -விலிருந்து வரையப்படும் கோடு இதற்கான வெக்டர்.

இவ்விரு கோடுகளும் இணையுமிடத்தில் உருவாவதே கோணம் ஆகும். அவை எந்த அளவுக்கு கோணலாக இணைகின்றனவோ, அதைப் பொறுத்து அதன் கோணமும், அக்கோடுகளின் திசையும் மாறுபடும்.

• சற்று முன்னோக்கி இணைவது 45 டிகிரி – ஓரளவுக்கு ஒரே திசை
• நெட்டு குத்தாக இணைந்தால் 90 டிகிரி – ஒரே திசையல்ல
• பின்னோக்கிச் சாய்வது 135 டிகிரி – சற்று எதிரான திசை
• நெட்டாக இணைவது 180 டிகிரி – முற்றிலும் எதிர் திசை

என 0 முதல் 360 வரை அதன் கோண மதிப்பு மாறுபடும். அம்மதிப்பினை பொறுத்து அந்த வெக்டர்களின் திசையை நாம் தெரிந்து கொள்ளலாம். நம்முடைய முக்கோணத்தில் sin,cos,tan எனப் பெயரிடப்பட்ட மூன்று கோணமதிப்புகளில், cos என்பதுதான் நமது வெக்டர்களின் திசையை கணிக்க உதவும் கோணம் ஆகும்.
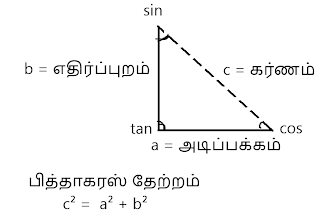
“இரு கோடுகள் இணைவதால் ஒரு கோணம் தானே ஏற்படுகிறது; பிறகு ஏன் முக்கோணம்?” என யோசிக்கிறீர்களா! இணைகின்ற இரு கோடுகளின் நீளத்திற்கு ஏற்ப எதிரே உருவாகும் ஒரு குறுக்குக் கோடே அதனை முக்கோணமாக்கியது. அதற்கு கர்ணம் என்று பெயர். இணைகின்ற இரு கோடுகளில் ஒன்று அடிப்பக்கம் என்றும், மற்றொன்று எதிர்ப்புறம் என்றும் அழைக்கப்படும். இந்த மூன்று கோடுகளின் நீளத்துக்குமான தொடர்பை விளக்குவதே பித்தாகரஸ் தேற்றம் ஆகும்.

sin, cos, tan

நாம் பார்க்கின்ற கோணத்தை பொறுத்து நமது கருத்து மாறுபடும் என்று கூறுவார்கள் அல்லவா! அதைப்போலத் தான், இந்த sin, cos, tan என்பதும்! ஒவ்வொன்றும் நமது முக்கோணத்தை ஒவ்வொரு கோணத்திலிருந்து அணுகி தனது கருத்தை தெரிவிக்கின்றது.

• sin என்பது செங்குத்து கோட்டினைப் பொறுத்து மற்றொரு கோடு எவ்வளவு தூரம் விலகுகிறது என்பதை அறிவிக்கிறது. கோபுரத்தின் உயரத்திலிருந்து சரிவான ஒரு சுற்றுச்சுவர் அமைப்பது போன்ற இடங்களில் இந்தக் கணக்கீடு உதவும்.
• tan என்பது கிடைமட்டக் கோட்டினைப் பொறுத்து மற்றொரு கோடு எவ்வளவு தூரம் விலகுகிறது என்பதை அறிவிக்கிறது. கிடைமட்டத் தரையிலிருந்து சாய்வான ஒரு மேம்பாலம் அமைப்பது போன்ற இடங்களில் இது கணக்கிடப்படும்.
• cos என்பது தான் கர்ணத்தின் நீளம் மற்றும் இரு பக்கங்களின் நீளத்தைப் பொறுத்து அக்கோடுகள் எந்த அளவுக்கு விரிந்துள்ளன என்பதை விளக்கும். இவ்விரு கோடுகளும் ஒன்றின் மேல் ஒன்றாக அமைந்திருந்தால் அதற்கிடையே எந்த ஒரு கோணமும் இருக்காது. அதுவே cos(0). இது 1 எனும் மதிப்பை வெளிப்படுத்தும். அவ்வாறே, cos(90) = 0 & cos(180) = -1 ஆகும்.

ஆகவே,

• 1 அல்லது அதற்கு நெருங்கிய மதிப்புகளை வெளிப்படுத்தினால், அவை ஒரே திசையில் உள்ளன – அதாவது ஒரே மாதிரியான வார்த்தைகளை குறிக்கின்றன என்று அர்த்தம்.
• 0 அல்லது அதற்கு நெருங்கிய மதிப்புகளை வெளிப்படுத்தினால், அவை ஒரே திசையில் இல்லை. ஆகவே அவை குறிக்கின்ற வார்த்தைகளுக்கு சம்பந்தம் இல்லை என்று அர்த்தம்.
• -1 எனில் எதிரெதிர் வார்த்தைகளை குறிப்பதாக அர்த்தம்.

இதன் அடிப்படையில் வெக்டார் கணிதத்தில் கணக்கிடப்படும் cos மதிப்பு 1 முதல் -1 வரையிலான மதிப்புகளை வெளிப்படுத்தி அவ்வெக்டர்களுக்கிடையேயான உறவைக் குறிக்கிறது.

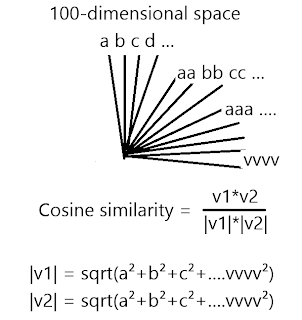
இதற்கான சூத்திரம் பின்வருமாறு. நம்முடைய எம்பெடிங் வெக்டரில் 100 எலிமெண்ட்ஸ் இருக்கும் என்பதால், இங்கு கற்பனையாக 100 அச்சுகள் கொண்ட வரைபடத்தை வரைந்து காட்டியுள்ளேன்.

இதில் |v1| என்பது வெக்டார் Magnitude எனப்படும் அதன் நீளத்தைக் குறிக்கும் குறியீடு ஆகும். இதைக் கண்டுபிடிக்க உதவும் சூத்திரமானது, பித்தாகரஸ் தேற்றத்தின் நீட்சியாக விளங்குவதை காணலாம். அதில் கர்ணத்தின் நீளத்தைக் கணக்கிட மற்ற இரண்டு பக்கங்களின் ஸ்கொயர் மதிப்பைக் கூட்டுவது போல, இங்கு அனைத்து பக்கங்களின் ஸ்கொயர் மதிப்பையும் கூட்டியுள்ளோம். வெக்டார் கணிதத்தில் மட்டும் எதற்காக cos மதிப்பைக் கணக்கிட, இரு வெக்டர்களும் அவைகளின் நீளமும் பெருக்கப்பட்டு வகுக்கப்படுகின்றன என்று யோசிக்கிறீர்களா? இதில் வெக்டர்களின் dot product -க்கான சமன்பாடு அதன் காஸ் மதிப்பையும் உள்ளடக்கியது.

v1.v2 = |v1|.|v2|. cos (theta)

ஆகவே cos மதிப்பை மட்டும் கணக்கிடுவதற்கான சமன்பாடு மேற்கண்டவாறு அமைந்து விடுகிறது.