AVL Trees / ஏவிஎல் மரம்
The AVL Tree is a type of Binary Search Tree named after two Soviet inventors Georgy Adelson-Velsky and Evgenii Landis who invented the AVL Tree in 1962.
AVL trees are self-balancing, which means that the tree height is kept to a minimum so that a very fast runtime is guaranteed for searching, inserting and deleting nodes, with time complexity O(logn)
ஏவிஎல் மரம் என்பது ஒரு வகை இருமத் தேடல் மரம் ஆகும். இது 1962-ல் ஏவிஎல் மரத்தைக் கண்டுபிடித்த ஜார்ஜி அடெல்சன்-வெல்ஸ்கி மற்றும் எவ்ஜெனி லாண்டிஸ் ஆகிய இரண்டு சோவியத் கண்டுபிடிப்பாளர்களின் பெயரால் அழைக்கப்படுகிறது.
ஏவிஎல் மரங்கள் சுய-சமநிலைப்படுத்தும் தன்மை கொண்டவை. இதன் பொருள், மரத்தின் உயரம் குறைந்தபட்ச அளவில் பராமரிக்கப்படுவதால், முனைகளைத் தேடுதல், செருகுதல் மற்றும் நீக்குதல் போன்ற செயல்பாடுகளுக்கு மிக வேகமான இயக்க நேரம் உறுதி செய்யப்படுகிறது. இதன் நேரச் சிக்கல்தன்மை O(log n) ஆகும்.
The only difference between a regular Binary Search Tree and an AVL Tree is that AVL Trees do rotation operations in addition, to keep the tree balance.
A Binary Search Tree is in balance when the difference in height between left and right subtrees is less than 2.
By keeping balance, the AVL Tree ensures a minimum tree height, which means that search, insert, and delete operations can be done really fast.
ஒரு சாதாரண பைனரி தேடல் மரம் மற்றும் ஒரு ஏவிஎல் மரத்திற்கு இடையேயான ஒரே வித்தியாசம் என்னவென்றால், ஏவிஎல் மரங்கள் மரத்தின் சமநிலையைப் பராமரிப்பதற்காகக் கூடுதலாகச் சுழற்சிச் செயல்பாடுகளைச் செய்கின்றன.
ஒரு பைனரி தேடல் மரத்தின் இடது மற்றும் வலது துணை மரங்களுக்கு இடையேயான உயர வேறுபாடு 2-ஐ விடக் குறைவாக இருக்கும்போது, அந்த மரம் சமநிலையில் இருப்பதாகக் கூறப்படுகிறது.
சமநிலையைப் பராமரிப்பதன் மூலம், ஏவிஎல் மரம் ஒரு குறைந்தபட்ச மர உயரத்தை உறுதி செய்கிறது. இதன் காரணமாக, தேடல், செருகுதல் மற்றும் நீக்குதல் போன்ற செயல்பாடுகளை மிக வேகமாகச் செய்ய முடியும்.
The two trees above are both Binary Search Trees, they have the same nodes, and the same in-order traversal (alphabetical), but the height is very different because the AVL Tree has balanced itself.
மேலே உள்ள இரண்டு மரங்களும் இருமத் தேடல் மரங்கள் ஆகும்; அவை ஒரே முனைகளைக் கொண்டுள்ளன, மேலும் அவற்றின் இன்-ஆர்டர் வரிசைப்படுத்தலும் (அகர வரிசைப்படி) ஒரே மாதிரியாக உள்ளது, ஆனால் ஏவிஎல் மரம் தன்னைத்தானே சமநிலைப்படுத்திக் கொண்டதால், அவற்றின் உயரம் மிகவும் வேறுபடுகிறது.
Left and Right Rotations
To restore balance in an AVL Tree, left or right rotations are done, or a combination of left and right rotations.
இடது மற்றும் வலது சுழற்சிகள்
ஒரு AVL மரத்தில் சமநிலையை மீட்டெடுக்க, இடது அல்லது வலது சுழற்சிகள் செய்யப்படுகின்றன, அல்லது இடது மற்றும் வலது சுழற்சிகளின் கலவை செய்யப்படுகிறது.
The Balance Factor
A node’s balance factor is the difference in subtree heights.
The subtree heights are stored at each node for all nodes in an AVL Tree, and the balance factor is calculated based on its subtree heights to check if the tree has become out of balance.
The height of a subtree is the number of edges between the root node of the subtree and the leaf node farthest down in that subtree.
சமநிலை காரணி
ஒரு முனையின் சமநிலை காரணி என்பது அதன் துணை மரங்களின் உயரங்களுக்கு இடையிலான வேறுபாடு ஆகும்.
ஒரு AVL மரத்தில் உள்ள அனைத்து முனைகளுக்கும், துணை மரங்களின் உயரங்கள் ஒவ்வொரு முனையிலும் சேமிக்கப்படுகின்றன, மேலும் மரம் சமநிலையற்றதாகிவிட்டதா என்பதைச் சரிபார்க்க, அதன் துணை மரங்களின் உயரங்களின் அடிப்படையில் சமநிலை காரணி கணக்கிடப்படுகிறது.
ஒரு துணை மரத்தின் உயரம் என்பது, அந்த துணை மரத்தின் மூல முனைக்கும், அந்த துணை மரத்தில் மிகக் கீழே உள்ள இலை முனைக்கும் இடையே உள்ள விளிம்புகளின் எண்ணிக்கை ஆகும்.
The Balance Factor (BF)
The Balance Factor (BF) for a node (X) is the difference in height between its right and left subtrees.
BF(X) = height(rightSubtree(X)) – height(leftSubtree(X))
Balance factor values
- 0: The node is in balance.
- more than 0: The node is “right heavy”.
- less than 0: The node is “left heavy”.
If the balance factor is less than -1, or more than 1, for one or more nodes in the tree, the tree is considered not in balance, and a rotation operation is needed to restore balance.
சமநிலை காரணி (BF)
ஒரு முனையின் (X) சமநிலை காரணி (BF) என்பது அதன் வலது மற்றும் இடது துணை மரங்களின் உயரங்களுக்கு இடையிலான வேறுபாடு ஆகும்.
BF(X) = உயரம்(வலது துணைமரம்(X)) – உயரம்(இடது துணைமரம்(X))
சமநிலை காரணி மதிப்புகள்:
- 0: முனை சமநிலையில் உள்ளது.
- 0-ஐ விட அதிகம்: முனை “வலதுபுறம் கனமாக” உள்ளது.
- 0-ஐ விடக் குறைவு: முனை “இடதுபுறம் கனமாக” உள்ளது.
மரத்திலுள்ள ஒன்று அல்லது அதற்கு மேற்பட்ட முனைகளுக்கு சமநிலை காரணி -1-ஐ விடக் குறைவாகவோ அல்லது 1-ஐ விட அதிகமாகவோ இருந்தால், அந்த மரம் சமநிலையில் இல்லை என்று கருதப்படுகிறது, மேலும் சமநிலையை மீட்டெடுக்க ஒரு சுழற்சி செயல்பாடு தேவைப்படுகிறது.
The Four “out-of-balance” Cases
When the balance factor of just one node is less than -1, or more than 1, the tree is regarded as out of balance, and a rotation is needed to restore balance.
There are four different ways an AVL Tree can be out of balance, and each of these cases require a different rotation operation.
சமநிலையற்ற நான்கு நிலைகள்
ஏதேனும் ஒரு முனையின் சமநிலை காரணி -1-ஐ விடக் குறைவாகவோ அல்லது 1-ஐ விட அதிகமாகவோ இருந்தால், அந்த மரம் சமநிலையற்றதாகக் கருதப்படுகிறது, மேலும் சமநிலையை மீட்டெடுக்க ஒரு சுழற்சி தேவைப்படுகிறது.
ஒரு AVL மரம் சமநிலையற்று இருக்க நான்கு வெவ்வேறு வழிகள் உள்ளன, மேலும் இந்த ஒவ்வொரு நிலைக்கும் ஒரு வெவ்வேறு சுழற்சி செயல்பாடு தேவைப்படுகிறது.
Left-Left (LL)
The unbalanced node and its left child node are both left-heavy.
Rotation to Restore Balance : A single right rotation.
இடம்-இடம் (LL)
சமநிலையற்ற முனையும் அதன் இடது குழந்தை முனையும் இரண்டும் இடதுபுறம் கனமாக உள்ளன. சமநிலையை மீட்டெடுப்பதற்கான சுழற்சி: ஒரு ஒற்றை வலதுபுறச் சுழற்சி.
Example:
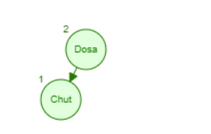
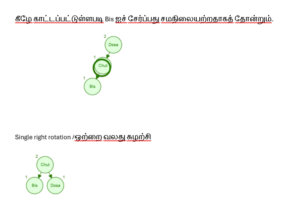
Add Bis will look unbalanced as shown below
கீழே காட்டப்பட்டுள்ளபடி Bis ஐச் சேர்ப்பது சமநிலையற்றதாகத் தோன்றும்.
Single right rotation /ஒற்றை வலது சுழற்சி
Right-Right (RR)
The unbalanced node and its right child node are both right-heavy.
Rotation to Restore Balance :A single left rotation.
வலது-வலது (RR)
சமநிலையற்ற முனையும் அதன் வலது குழந்தை முனையும் இரண்டும் வலதுபுறம் கனமாக உள்ளன.
சமநிலையை மீட்டெடுப்பதற்கான சுழற்சி: ஒரு ஒற்றை இடதுபுறச் சுழற்சி.
Example:
Insert Idly on above tree, right side is heavy /மேலே உள்ள மரத்தில் இட்லியைச் செருகவும், வலது பக்கம் கனமாக உள்ளது.
Single left rotation make AVL tree balanced / ஒற்றை இடது சுழற்சி ஏவிஎல் மரத்தை சமநிலைப்படுத்துகிறது.
Left-Right (LR)
The unbalanced node is left heavy, and its left child node is right heavy.
Rotation to Restore Balance : First do a left rotation on the left child node, then do a right rotation on the unbalanced node.
இடம்-வலம் (LR)
சமநிலையற்ற முனை இடதுபுறம் கனமாக உள்ளது, மேலும் அதன் இடது குழந்தை முனை வலதுபுறம் கனமாக உள்ளது.
சமநிலையை மீட்டெடுப்பதற்கான சுழற்சி: முதலில் இடது குழந்தை முனையில் ஒரு இடதுபுறச் சுழற்சியைச் செய்யவும், பின்னர் சமநிலையற்ற முனையில் ஒரு வலதுபுறச் சுழற்சியைச் செய்யவும்.
Example:
Insert Dosa to above AVL Tree which is unbalanced /சமநிலையற்ற நிலையில் உள்ள மேற்கண்ட AVL மரத்தில் ‘தோசை’ என்ற சொல்லைச் செருகவும்.
In this LR case, a left rotation is first done on the left child node, and then a right rotation is done on the original unbalanced node.
இந்த LR நிலையில், முதலில் இடது குழந்தைப் புள்ளி மீது ஒரு இடது சுழற்சியும், பின்னர் அசல் சமநிலையற்ற புள்ளி மீது ஒரு வலது சுழற்சியும் செய்யப்படுகிறது.
The Right-Left (RL) Case
The Right-Left case is when the unbalanced node is right heavy, and its right child node is left heavy.
In this case we first do a right rotation on the unbalanced node’s right child, and then we do a left rotation on the unbalanced node itself.
வலது-இடது (RL) நிலை
வலது-இடது நிலை என்பது, சமநிலையற்ற முனை வலதுபுறம் கனமாக இருப்பதும், அதன் வலது குழந்தை முனை இடதுபுறம் கனமாக இருப்பதும் ஆகும்.
இந்த நிலையில், நாம் முதலில் சமநிலையற்ற முனையின் வலது குழந்தை முனையில் ஒரு வலது சுழற்சியைச் செய்கிறோம், பின்னர் சமநிலையற்ற முனையிலேயே ஒரு இடது சுழற்சியைச் செய்கிறோம்.
After inserting node Egg, we get a Right-Left case because node Dosa becomes unbalanced and right heavy, and its right child is left heavy. (First image) To restore balance, a right rotation is first done on node Grap, and then a left rotation is done on node Dosa.
எக் (Egg) நோடைச் செருகிய பிறகு, நோட் டோசா சமநிலையற்றதாகவும், வலதுபுறம் கனமாகவும் மாறுவதாலும், அதன் வலதுபுறச் சைல்டு இடதுபுறம் கனமாக இருப்பதாலும், நமக்கு ஒரு வலது-இடது நிலை ஏற்படுகிறது. (முதல் படம்) சமநிலையை மீட்டெடுக்க, முதலில் கிராப் (Grap) நோடில் ஒரு வலது சுழற்சியும், பின்னர் டோசா (Dosa) நோடில் ஒரு இடது சுழற்சியும் செய்யப்படுகிறது.
Retracing in AVL Trees
After inserting or deleting a node in an AVL tree, the tree may become unbalanced. To find out if the tree is unbalanced, we need to update the heights and recalculate the balance factors of all ancestor nodes.
This process, known as retracing, is handled through recursion. As the recursive calls propagate back to the root after an insertion or deletion, each ancestor node’s height is updated and the balance factor is recalculated. If any ancestor node is found to have a balance factor outside the range of -1 to 1, a rotation is performed at that node to restore the tree’s balance.
AVL மரங்களில் பின்னோக்கிச் செல்லுதல்
ஒரு AVL மரத்தில் ஒரு முனையைச் செருகிய அல்லது நீக்கிய பிறகு, அந்த மரம் சமநிலையற்றதாக மாறக்கூடும். மரம் சமநிலையற்றதாக உள்ளதா என்பதைக் கண்டறிய, நாம் அனைத்து மூதாதை முனைகளின் உயரங்களையும் புதுப்பித்து, சமநிலை காரணிகளை மீண்டும் கணக்கிட வேண்டும்.
பின்னோக்கிச் செல்லுதல் என்று அழைக்கப்படும் இந்தச் செயல்முறை, மீள்சுழற்சி மூலம் கையாளப்படுகிறது. ஒரு செருகல் அல்லது நீக்கத்திற்குப் பிறகு மீள்சுழற்சி அழைப்புகள் வேர் முனைக்குத் திரும்பும்போது, ஒவ்வொரு மூதாதை முனையின் உயரமும் புதுப்பிக்கப்பட்டு, சமநிலை காரணி மீண்டும் கணக்கிடப்படுகிறது. ஏதேனும் ஒரு மூதாதை முனையின் சமநிலை காரணி -1 முதல் 1 வரையிலான வரம்பிற்கு வெளியே இருப்பது கண்டறியப்பட்டால், மரத்தின் சமநிலையை மீட்டெடுக்க அந்த முனையில் ஒரு சுழற்சி செய்யப்படுகிறது.
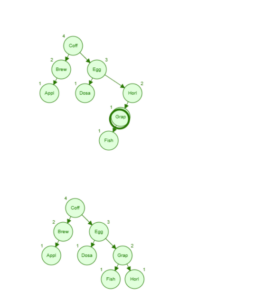
After inserting node Fish, the nodes Coff, Egg and Horl are all unbalanced, but since retracing works through recursion, the unbalance at node Horl is discovered and fixed first, which in this case also fixes the unbalance in nodes Egg and Coff
Fishமுனையைச் செருகிய பிறகு, Coff, Egg மற்றும் Horl முனைகள் அனைத்தும் சமநிலையற்றவை, ஆனால் மறுபரிசீலனை மறுநிகழ்வு மூலம் செயல்படுவதால், முனை Horl உள்ள சமநிலையின்மை முதலில் கண்டறியப்பட்டு சரி செய்யப்படுகிறது, இது இந்த விஷயத்தில் முட்டை மற்றும் Coff முனைகளிலும் உள்ள சமநிலையின்மையை சரிசெய்கிறது.
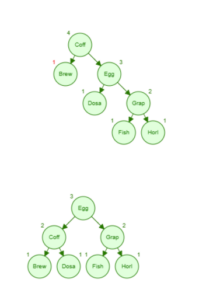
After node Fish is inserted, the code will retrace, calculating balancing factors as it propagates back up towards the root node. When node Horl reached and the balancing factor -2 is calculated, a right rotation is done. Only after this rotation is done, the code will continue to retrace, calculating balancing factors further up on ancestor nodes Egg and Coff.
Because of the rotation, balancing factors for nodes Egg and Coff stay the same as before node Fish was inserted.
Fish முனைமம் செருகப்பட்ட பிறகு, குறியீடு மீண்டும் பின்னோக்கிச் சென்று, மூல முனைமத்தை நோக்கி மேலே பரவும்போது சமநிலைப்படுத்தும் காரணிகளைக் கணக்கிடும். Horl முனைமத்தை அடைந்து, சமநிலைப்படுத்தும் காரணி -2 எனக் கணக்கிடப்பட்டதும், ஒரு வலதுபுறச் சுழற்சி செய்யப்படுகிறது. இந்தச் சுழற்சி செய்யப்பட்ட பின்னரே, குறியீடு மீண்டும் பின்னோக்கிச் சென்று, அதன் மூதாதை முனைமங்களான Egg மற்றும் Coff ஆகியவற்றில் உள்ள சமநிலைப்படுத்தும் காரணிகளைக் கணக்கிடும்.
Insert Node
The implementation below builds an AVL tree based on a list of food items, to create the AVL Tree in the simulation above. The last node to be inserted ‘Fish’, also triggers a right rotation, just like in the simulation above.
முனையைச் செருகுதல்
கீழே உள்ள செயலாக்கம், மேலே உள்ள உருவகப்படுத்துதலில் AVL மரத்தை உருவாக்குவதற்காக, உணவுப் பொருட்களின் பட்டியலின் அடிப்படையில் ஒரு AVL மரத்தை உருவாக்குகிறது. செருகப்பட வேண்டிய கடைசி முனையான ‘மீன்’, மேலே உள்ள உருவகப்படுத்துதலில் உள்ளதைப் போலவே, ஒரு வலதுபுறச் சுழற்சியைத் தூண்டுகிறது.
Example:
class TreeNode:
def init(self, data):
self.data = data
self.left = None
self.right = None
self.height = 1
def getHeight(node):
if not node:
return 0
return node.height
def getBalance(node):
if not node:
return 0
return getHeight(node.left) – getHeight(node.right)
def rightRotate(y):
print(‘Rotate right on node’,y.data)
x = y.left
T2 = x.right
x.right = y
y.left = T2
y.height = 1 + max(getHeight(y.left), getHeight(y.right))
x.height = 1 + max(getHeight(x.left), getHeight(x.right))
return x
def leftRotate(x):
print(‘Rotate left on node’,x.data)
y = x.right
T2 = y.left
y.left = x
x.right = T2
x.height = 1 + max(getHeight(x.left), getHeight(x.right))
y.height = 1 + max(getHeight(y.left), getHeight(y.right))
return y
def insert(node, data):
if not node:
return TreeNode(data)
if data < node.data:
node.left = insert(node.left, data)
elif data > node.data:
node.right = insert(node.right, data)
Update the balance factor and balance the tree
node.height = 1 + max(getHeight(node.left), getHeight(node.right))
balance = getBalance(node)
Balancing the tree
Left Left
if balance > 1 and getBalance(node.left) >= 0:
return rightRotate(node)
Left Right
if balance > 1 and getBalance(node.left) < 0:
node.left = leftRotate(node.left)
return rightRotate(node)
Right Right
if balance < -1 and getBalance(node.right) <= 0:
return leftRotate(node)
Right Left
if balance < -1 and getBalance(node.right) > 0:
node.right = rightRotate(node.right)
return leftRotate(node)
return node
def inOrderTraversal(node):
if node is None:
return
inOrderTraversal(node.left)
print(node.data, end=”, “)
inOrderTraversal(node.right)
Inserting nodes
root = None
letters = [‘Coff’, ‘Brew’, ‘Egg’, ‘Appl’, ‘Dosa’, ‘Horl’, ‘Grap’, ‘Fish’]
for letter in letters:
root = insert(root, letter)
inOrderTraversal(root)
Output:
Rotate right on node Horl
Appl, Brew, Coff, Dosa, Egg, Fish, Grap, Horl
Delete Node
To delete a node in an AVL Tree, the same code to restore balance is needed as for the code to insert a node.
முனையை நீக்கு
AVL மரத்தில் ஒரு முனையை நீக்க, சமநிலையை மீட்டெடுக்க ஒரு முனையைச் செருகுவதற்கான குறியீட்டிற்குத் தேவைப்படும் அதே குறியீடு தேவை.
Example
class TreeNode:
def init(self, data):
self.data = data
self.left = None
self.right = None
self.height = 1
def getHeight(node):
if not node:
return 0
return node.height
def getBalance(node):
if not node:
return 0
return getHeight(node.left) – getHeight(node.right)
def rightRotate(y):
x = y.left
T2 = x.right
x.right = y
y.left = T2
y.height = 1 + max(getHeight(y.left), getHeight(y.right))
x.height = 1 + max(getHeight(x.left), getHeight(x.right))
return x
def leftRotate(x):
y = x.right
T2 = y.left
y.left = x
x.right = T2
x.height = 1 + max(getHeight(x.left), getHeight(x.right))
y.height = 1 + max(getHeight(y.left), getHeight(y.right))
return y
def insert(node, data):
if not node:
return TreeNode(data)
if data < node.data:
node.left = insert(node.left, data)
elif data > node.data:
node.right = insert(node.right, data)
Update the balance factor and balance the tree
node.height = 1 + max(getHeight(node.left), getHeight(node.right))
balance = getBalance(node)
Balancing the tree
Left Left
if balance > 1 and getBalance(node.left) >= 0:
return rightRotate(node)
Left Right
if balance > 1 and getBalance(node.left) < 0:
node.left = leftRotate(node.left)
return rightRotate(node)
Right Right
if balance < -1 and getBalance(node.right) <= 0:
return leftRotate(node)
Right Left
if balance < -1 and getBalance(node.right) > 0:
node.right = rightRotate(node.right)
return leftRotate(node)
return node
def inOrderTraversal(node):
if node is None:
return
inOrderTraversal(node.left)
print(node.data, end=”, “)
inOrderTraversal(node.right)
def minValueNode(node):
current = node
while current.left is not None:
current = current.left
return current
def minValueNode(node):
current = node
while current.left is not None:
current = current.left
return current
def delete(node, data):
if not node:
return node
if data < node.data:
node.left = delete(node.left, data)
elif data > node.data:
node.right = delete(node.right, data)
else:
if node.left is None:
temp = node.right
node = None
return temp
elif node.right is None:
temp = node.left
node = None
return temp
temp = minValueNode(node.right)
node.data = temp.data
node.right = delete(node.right, temp.data)
if node is None:
return node
Update the balance factor and balance the tree
node.height = 1 + max(getHeight(node.left), getHeight(node.right))
balance = getBalance(node)
Balancing the tree
Left Left
if balance > 1 and getBalance(node.left) >= 0:
return rightRotate(node)
Left Right
if balance > 1 and getBalance(node.left) < 0:
node.left = leftRotate(node.left)
return rightRotate(node)
Right Right
if balance < -1 and getBalance(node.right) <= 0:
return leftRotate(node)
Right Left
if balance < -1 and getBalance(node.right) > 0:
node.right = rightRotate(node.right)
return leftRotate(node)
return node
Inserting the food items
root = None
foods = [‘Coff’, ‘Brew’, ‘Egg’, ‘Appl’, ‘Dosa’, ‘Horl’, ‘Grap’, ‘Fish’]
for food in foods:
root = insert(root, food)
inOrderTraversal(root)
print(‘\nDeleting Appl’)
root = delete(root,’Appl’)
inOrderTraversal(root)
Output:
Appl, Brew, Coff, Dosa, Egg, Fish, Grap, Horl,
Deleting Appl
Brew, Coff, Dosa, Egg, Fish, Grap, Horl,